変換行列

上記のステップ2の変換行列には PCi_j と CDi_j の2つのキーワードのどちらかが使われる。 これは WCS の paper をまとめる過程で、CDELTi とキーワードPCで表される PC行列で記述する案に対して、HST と IRAF ではキーワード CDで表される CD行列が既に使われていたことから、両方を併記することになったのである。

PCi_j 形式では、変換行列の要素 $m_{ij}$ はヘッダーの PCi_j (浮動小数) で表され、$s_i$ は CDELTi で表される。 $i$ や $j$ は 1から始まり(例えば PC1_1とかCDELT1)、デフォルトの PCi_j の値は $i = j$ に対して 1.0 それ以外は 0.0 である。 PCi_j 行列は正則行列で逆行列を持たなければならず、CDELTi は 0であってはならない。

$$\left ( \begin{array}{c} q_1 \\ q_2 \\ q_3 \\ \vdots \end{array} ... ...in{array}{c} p_1 - r_1 \\ p_2 - r_2 \\ p_3 - r_3 \\ \vdots \end{array} \right )$$

中間世界座標の $x_i$ は前述のとおり $x_i = s_i q_i = \texttt{CDELT}i q_i$ で計算される。

一方、CDi_j 形式では、式 (16) と (17) は一緒になって、

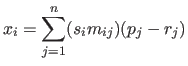$$x_i = \sum^n_{j=1}(s_im_{ij})(p_j - r_j)$$ (18)

となり、積 $s_im_{ij}$ が CDi_j (浮動小数) で表される。 $i$ や $j$ は 1から始まり(例えば CD1_1)、CDi_j 行列は正則行列で逆行列を持たなければならない。

$$\left ( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \end{array} ... ...in{array}{c} p_1 - r_1 \\ p_2 - r_2 \\ p_3 - r_3 \\ \vdots \end{array} \right )$$

古いソフトウェアのために、CDELTi や CROTAi は CDi_j と共存することが許されるが、新しいソフトウェアではこれらは無視されるべきである。 CDi_j と PCi_j のデフォルトの振る舞いは異なり、もし 1枚以上の CDi_j キーワードレコードが存在すれば、存在しない CDi_j は 0とみなされる。 一方、CDi_j が存在しない場合は、PCi_j キーワードレコードが存在しなくても、PCi_j 形式が仮定される(これは Wells らによるFITS の原論文(4.1節 の FITS Paper I)のCDELTi の解釈と一致する)。 PCi_j と CDi_j の混在は禁止される。 このため、CDi_j 形式と PCi_j 形式の変換は単純にキーワードの置き換えで行われ、CDi_j は PCi_j と同値で CDELTi は 1と見なされ、逆の場合は PCi_j と CDELTi から CDi_j が計算される。