$(\phi, \theta) \Rightarrow (R_{\theta}, \phi) \quad {\rm or 一般に} \quad (x, y)$

　

次に射影による局所 (native) 球面座標から平面上の座標への変換を行う。

射影平面上に球面との接点を中心とする極座標 $(R_{\theta}, A_{\phi})$ を設定する。 $A_{\phi}$ は軸を適当にとることにより $\phi = A_{\phi}$ とすることができるので、$\theta$ と $R_{\theta}$ の関係として射影を記述できることになる。

局所球面座標の $(x, y)$ 座標に対する位置関係を 2つの典型的なケース (平面が極で接する場合と赤道面 (の基準経度) で接する場合) について表示したのが次ページの図4である。

=1mm

図 4: 参照点を極とした局所 (native) 球面座標 (左、 $(\phi _0, \theta _0)=(0,90^\circ )$) と、参照点を赤道と基準経度の交点とした局所球面座標 (右、 $(\phi _0, \theta _0)=(0,0)$)

ここでは接平面への射影 (Zenithal projection) の一般形およびそのうちの代表的な もの 4つについて述べる。

〔一般形 (AZP)〕

射影の投影中心は球面と投影面の接点と球面の中心を通る直線上にあり、その球面 中心からの距離を$\mu$とすると、 $R_{\theta}$と$\theta$の関係は

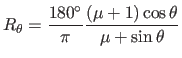$$R_{\theta} = \frac{180^{\circ}}{\pi} \frac{(\mu+1)\cos\theta}{\mu+\sin\theta}$$ (20)

となる。投影中心の位置 ($\mu$の値) により射影の性質が完全に決まる (次の図)。

=1mm

図 5: zenithal 投影の $R_{\theta }, \theta , \mu$の関係図 (左)、と 3 つの特別なケース (右)

以下で、代表的な 4つの射影方法を示す。

〔AZP ($\mu=0$): TAN:gnomonic〕

$\mu=0$: 球面の中心が投影の中心になっている場合で、可視光の撮像観測は このケースにあたる (以前の提案では TAN が機器の distortion を含む拡張した形になっていたが、機器の distortion は WCS Paper V で扱うように分離された)。

〔STG:stereographic〕

$\mu=1$: 球面の平面から反対の端点が投影の中心になっている特別な場合。

〔AZP ( $\mu=\infty$): orthographic $\subset$ SIN:slant orthographic〕

$\mu=\infty$: 無限遠方からの投影である。電波干渉計によるマッピング 観測はこのケースになる (以前はこのケースは SIN と呼ばれていたが、SINは Greisen が AIPS Memo (1983) で NCPと呼んだ東西方向の干渉計も扱えるように拡張された)。

〔ARC: zenithal equidistance〕

シュミット望遠鏡の場合、 $R_{\theta}$と$\theta$の関係が特殊で、 $R_{\theta} = (90^\circ - \theta)$となっている。

$(R_{\theta}, \phi)$から$(x, y)$への変換は次式による。

$$x = R_{\theta}\sin\phi$$ (21)

$$y = -R_{\theta}\cos\phi$$ (22)

(逆は $\phi=\arg(-y, x), R_{\theta}=\sqrt{x^2+y^2}$ )。

ここまでに出てきた変数を(関係するFITS キーワードを含めて)表にまとめておく。

変数	意味	関係するFITS キーワード
$i$	世界座標のインデックス
$j$	ピクセル座標のインデックス
$a$	代替記述コード(空白かA - Z)
$p_j$	ピクセル座標
$r_j$	参照ピクセル座標	CRPIXja
$m_{ij}$	線形変換行列	CDi_ja or PCi_ja
$s_i$	座標スケール	CDELTia
$x_i$	中間世界座標(一般形)
$(x, y)$	射影平面座標
$(\phi, \theta)$	局所(native)経度、緯度
$(\alpha , \delta )$	天球経度、緯度
$(\phi_0, \theta_0)$	接点の局所(native)経度、緯度	PV$i\_1a$, PV$i\_2a$
$(\alpha_0, \delta_0)$	接点の天球経度、緯度	CRVALia
$(\phi_P, \theta_P)$	天球の極の局所(native)経度、緯度	LONPOLEa(=PV$i\_3a$), LATPOLEa(=PV$i\_4a$)
$(\alpha_P, \delta_P)$	局所(native)極の天球経度、緯度( $\delta_p=\theta_p$)
arg()	正確な象限を返す tangent の逆関数

以上をふまえ、射影平面座標から天球座標を求めるための FITS パラメータとその使用法を次項で述べる。