WCS で記述された天球座標の解釈の具体例

次のページの表12のようなヘッダのファイルを例に具体的な計算例を示す。

表 13: Example FITS header with coordinates

これは通常の光学イメージのファイルであり、 $512ピクセル\times 512ピクセル\times 196プレーン (+ 偏光が1)$ からなることがわかる。

CRPIXjキーワードから参照点はピクセル座標の (256, 257, 1, 1) であり、PCi_jaキーワードがない(=デフォルトの単位行列) ことから回転や曲がりはないことがわかる。

これらのことから中間世界座標は次のようにして求められる。

$$\left ( \begin{array}{c} x \\ y \\ z \\ s \end{array} \right ) = ... ...rray}{c} p_1 - 256 \\ p_2 - 257 \\ p_3 - 1 \\ p_4 - 1 \end{array} \right ) \, .$$ (23)

次に 'VELOCITY' と 'STOKES' は線形軸なので簡単に計算でき、次のようになる。

$$Velocity = 500000.0 + 7128.3 (p_3 - 1)\: {\rm ms}^{-1},$$ (24)

$$Stokes = 1 (I {\rm polarization})$$ (25)

CTYPE1 と CTYPE2 によれば、座標の投影法が TAN (gnomonic) なので、zenithal 投影であり、

$$\phi = \arg\,(-y,x) = \arg\,(p_2-257,p_1-256) + 180^{\circ}$$ (26)

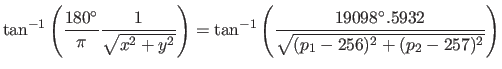$$\theta = \tan^{-1} \left ( \frac{180^{\circ}}{\pi}\frac{1}{\sqrt{x^2+y^2}}... ...{-1} \left ( \frac{19098^{\circ}.5932}{\sqrt{ (p_1-256)^2+(p_2-257)^2}} \right)$$ (27)

で native 座標の経度、緯度が計算できる¹⁸。 CTYPEia が RA と DEC で始まっているので赤道座標であり、 RADESYSa, EQUINOXa により、IAU 1984 システムであることがわかる。 また、参照点は zenithal 投影なので native 座標の北極であり、それに対する CRVALi により $\alpha_P = 45^{\circ}.83$, $\delta_P = 63^{\circ}.57$ である。

赤道座標の北極は native 座標の経度 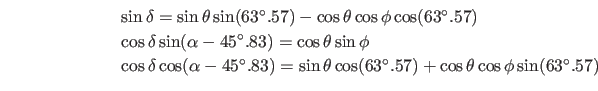$180^{\circ}$ であることが LONPOLEa からわかるので、赤経・赤緯は、(19)式から、

$$\begin{array}{l} \sin\delta = \sin\theta \sin(63^{\circ}.57) ... ...{\circ}.57) + \cos\theta\cos\phi\sin(63^{\circ}.57) \end{array}$$ (28)

となり、結局イメージの 3つの隅の座標は、

パラメータ	単位	SEの隅	NEの隅	NWの隅
$(p_1,p_2)$	pixels	(1, 2)	(1, 512)	(511, 512)
$(p_3,p_4)$	pixels	(1, 1)	(1, 1)	(196, 1)
$x$	deg	$0^{\circ}.765000$	$0^{\circ}.765000$	$-0^{\circ}.765000$
$y$	deg	$-0^{\circ}.765000$	$0^{\circ}.765000$	$0^{\circ}.765000$
$\phi$	deg	$45^{\circ}.000000$	$135^{\circ}.000000$	$225^{\circ}.000000$
$\theta$	deg	$88^{\circ}.918245$	$88^{\circ}.918255$	$88^{\circ}.918255$
$\alpha$	deg	$47^{\circ}.503264$	$47^{\circ}.595581$	$44^{\circ}.064419$
$\delta$	deg	$62^{\circ}.795111$	$64^{\circ}.324332$	$64^{\circ}.324332$
Velocity	ms$^{-1}$	500000.00	500000.00	1890018.50
Stokes		$1.0 \equiv$ I	$1.0 \equiv$ I	$1.0 \equiv$ I

となる。

ここでは WCS で書かれた FITS ヘッダの解釈の例を上げたが、原論文には実際の観測データを WCS を使った FITS ファイルにどう書くかについても例が挙げてある (例えば COBE/DIRBE や ロングスリット のデータの WCS ヘッダの構築法など)。 興味のある方は参照されたい。