Next: 座標パラメータ Up: 分光座標の計算 Previous: 対数線形座標
ここでは、ある軸がスペクトル変数![]() で線形にサンプリングされ、変数
で線形にサンプリングされ、変数![]() で表現される場合を考える。
スペクトル変数としては様々な組み合わせが考えられ、どの組み合わせも非線形でありうるが、どのスペクトル変数も
で表現される場合を考える。
スペクトル変数としては様々な組み合わせが考えられ、どの組み合わせも非線形でありうるが、どのスペクトル変数も
![]() のどれかと線形に結びつく。
これでもまだ多くの組み合わせがありうるので、
のどれかと線形に結びつく。
これでもまだ多くの組み合わせがありうるので、![]() と線形関係にある基本変数
と線形関係にある基本変数
![]() のどれかを表す中間変数
のどれかを表す中間変数 ![]() を導入して計算方法を考えてみる。
を導入して計算方法を考えてみる。
![]() とその逆関係
とその逆関係 ![]() は基本変数
は基本変数
![]() の関係として次の左表のように表され、
の関係として次の左表のように表され、![]() とその逆関係の
とその逆関係の ![]() は次の右表のような関係となる。
は次の右表のような関係となる。
|
|
![]() と
と ![]() の関係は中間変数である
の関係は中間変数である ![]() を介して
を介して
![]() と表される(逆関数は
と表される(逆関数は
![]() )。
)。
![]() は線形なので、
は線形なので、![]() と
と ![]() は常に異ならなければならない(そうでなければ
は常に異ならなければならない(そうでなければ 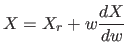 が線形になって非線形軸でなくなってしまう)。
このことから CTYPEka の最後の 3文字で使われる非線形アルゴリズムとしては次のようなものがあることになる。
が線形になって非線形軸でなくなってしまう)。
このことから CTYPEka の最後の 3文字で使われる非線形アルゴリズムとしては次のようなものがあることになる。
| コード | 通常以下でサンプリングされる | 以下で表現される |
| F2W | 周波数 | 波長 |
| F2V | 周波数 | 見かけの速度 |
| F2A | 周波数 | (空気中の)波長 |
| W2F | 波長 | 周波数 |
| W2V | 波長 | 見かけの速度 |
| W2A | 波長 | (空気中の)波長 |
| V2F | 見かけの速度 | 周波数 |
| V2W | 見かけの速度 | 波長 |
| V2A | 見かけの速度 | (空気中の)波長 |
| A2F | (空気中の)波長 | 周波数 |
| A2W | (空気中の)波長 | 波長 |
| A2V | (空気中の)波長 | 見かけの速度 |
| LOG | 対数 | どの座標タイプも可 |
| GRI | 検出器 | どの座標タイプも可 |
| GRA | 検出器 | どの座標タイプも可 |
| TAB | 通常ない | どの座標タイプも可 |
この 3文字コードの最初の 1文字は ![]() を表し、周波数(F)、波長(W)、(空気中の)波長(A)、見かけの速度(V) のどれかであり、3番目の文字は
を表し、周波数(F)、波長(W)、(空気中の)波長(A)、見かけの速度(V) のどれかであり、3番目の文字は ![]() を表す。
例えば、'ZOPT-F2W' の場合
を表す。
例えば、'ZOPT-F2W' の場合 ![]() は周波数、
は周波数、![]() は波長であり、この 2つの非線形変換は上左表により決まる。
最終的にスペクトル座標
は波長であり、この 2つの非線形変換は上左表により決まる。
最終的にスペクトル座標 ![]() として赤方偏移(ZOPT)を求めたいが、これは中間変数
として赤方偏移(ZOPT)を求めたいが、これは中間変数 ![]() (波長) と上右表の関係で結び付けられている。
(波長) と上右表の関係で結び付けられている。
線形にサンプリングされた ![]() からスペクトル座標
からスペクトル座標 ![]() を求める一般的な方法は次のようになる。
を求める一般的な方法は次のようになる。
![]() は線形にサンプリングされているので、
は線形にサンプリングされているので、
であり ![]() は定数である。この定数は、
は定数である。この定数は、
![]() という要求から決まる。これにより参照点では
という要求から決まる。これにより参照点では
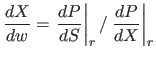 であることから、
であることから、
と計算できる。
![]() が逆関数の
が逆関数の
![]() と同様にわかっているとすると、
と同様にわかっているとすると、![]() を
を 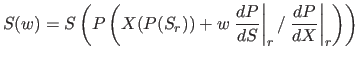 の関数として表せて、
の関数として表せて、
| (33) |
となる。
ここで ![]() は CRVALka で与えられる。
即ち、
は CRVALka で与えられる。
即ち、![]() を求めるには次の 3ステップを踏めばよい。
を求めるには次の 3ステップを踏めばよい。
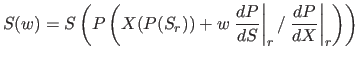 から
から 原論文には具体的な計算例もあるので参照されたい。
Osamu Kanamitsu